Введение в системы управления базами данных
Теперь каждое наименование встречается только
Пример 11
| 1 | Математика |
| 2 | Информатика |
| 3 | Физика |
Таблица 11 Отношение "Предметы"
Теперь каждое наименование встречается только в одном месте.
И все-таки как в исходном, так и в модифицированном отношении имеются аномалии обновления, возникающие при попытке вставить или удалить кортежи.
Аномалия вставки. При попытке добавить в отношение "Абитуриенты-Факультеты-Предметы" новый кортеж, например (Сидоров, Математический, Математика), мы обязаны добавить также и кортеж (Сидоров, Математический, Информатика), т.к. все абитуриенты математического факультета обязаны иметь один и тот же список сдаваемых предметов. Соответственно, при попытке вставить в модифицированное отношении кортеж (3, 1, 1), мы обязаны вставить в него также и кортеж (3, 1, 2).
Аномалия удаления. При попытке удалить кортеж (Иванов, Математический, Математика), мы обязаны удалить также и кортеж (Иванов, Математический, Информатика) по той же самой причине.
Таким образом, вставка и удаление кортежей не может быть выполнена независимо от других кортежей отношения.
Кроме того, если мы удалим кортеж (Иванов, Физический, Математика), а вместе с ним и кортеж (Иванов, Физический, Физика), то будет потеряна информация о предметах, которые должны сдаваться на физическом факультете.
Декомпозиция отношения "Абитуриенты-Факультеты-Предметы" для устранения указанных аномалий не может быть выполнена на основе функциональных зависимостей, т.к. это отношение не содержит никаких функциональных зависимостей. Это отношение является полностью ключевым, т.е. ключом отношения является все множество атрибутов. Но ясно, что какая-то взаимосвязь между атрибутами имеется. Эта взаимосвязь описывается понятием многозначной зависимости.
Определение 2. Пусть




Тогда атрибуты (множества атрибутов)



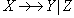

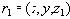
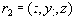

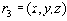
Замечание. Меняя местами кортежи



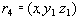




В отношении "Абитуриенты-Факультеты-Предметы" имеется многозначная зависимость Факультет

Словами это можно выразить так - для каждого факультета (для каждого значения из






Замечание. Если в отношении




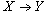
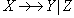
Действительно, действуя формально в соответствии с определением многозначной зависимости, предположим, что в отношении

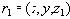
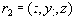
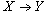
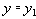
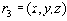
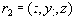

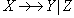
Таким образом, понятие многозначной зависимости является обобщением понятия функциональной зависимости.
Определение 3. Многозначная зависимость
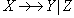
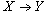
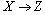
В отношении "Абитуриенты-Факультеты-Предметы" имеется именно нетривиальная многозначная зависимость Факультет

Теорема (Фейджина). Пусть



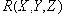
Декомпозиция отношения

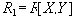
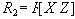
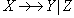
Замечание. Если зависимость
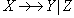
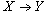
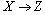
Доказательство теоремы.
Необходимость. Пусть декомпозиция отношения

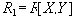
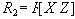
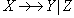
Предположим, что отношение

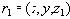
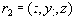
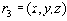

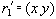
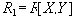
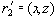
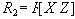
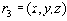
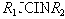

Достаточность. Пусть имеется многозначная зависимость
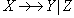

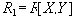
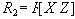
Как и в доказательстве теоремы Хеза, нужно доказать, что
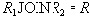

Включение
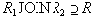

Докажем включение
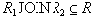
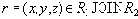
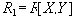
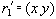
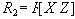
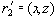



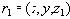



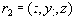
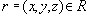
Определение 4. Отношение

Отношение "Абитуриенты-Факультеты-Предметы" находится в НФБК, но не в 4НФ. Согласно теореме Фейджина, это отношение можно без потерь декомпозировать на отношения:
